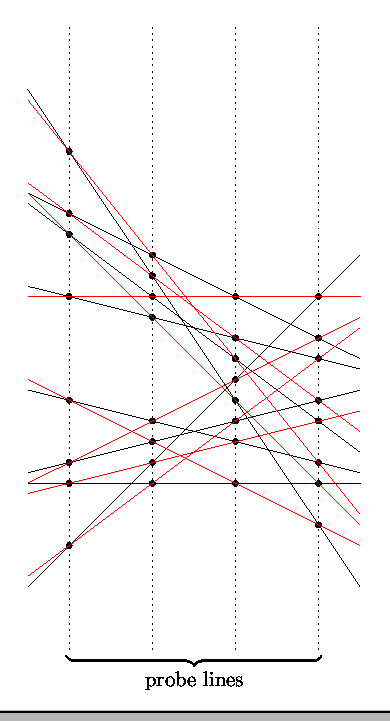
Suppose the only access we have to an arrangement of n input lines is to ``probe'' the arrangement with vertical lines. A probe returns the set of probe points which are the intersections of the probe's vertical line (the probe line) with all input lines. We will investigate when it is possible to determine the n input lines from the probe data. Below is an example of two arrangements of eight lines which produce the same probe data:

Suppose you are working over a field of rational functions over a finite field. How does one define a measure on this field? Is the field complete with respect to this measure? How could one define a Fourier transform? I will answer all of these questions. I will even define a function analogous to the classical theta function and give an application to number theory. This talk is intended to be an introduction. I will assume you have seen a measure and a Fourier transform before, but not much else.

The digit that a number begins with is not evenly distributed. More numbers begin with 1 than with 2, more with 2 than 3, and so on. I'll make this claim precise, explain why it is true, and describe applications in such important ongoing research areas as income tax evasion and winning the lottery.

Electrical Impedance Tomography is a technique that attemps to characterize the conductivity distribution inside a domain from boundary measurements. In a medical application, one applies a current and makes voltage measurements at the boundary. From this data, one tries to describe the conductivity of the interior (for example, tell the difference between the heart and the lungs based on their conductivity). There has been some discussion as to whether it's "better" to use dipole or trigonometic current patterns. This paper attemps to quantify the "information" content of the data obtained from each of the two current patterns using a least- squares solution and certain stability criteria.

There is a little known and greatly misunderstood option available for students pursuing a PhD in Mathematics - the Mathematics Education option. I will describe the program, answer frequently asked questions ("What kind of research do you do, anyway?"), and give an introduction to my own area of interest - using cryptography to teach algebraic concepts ranging from linear equations to group theory. I will also describe how you can make yourself more marketable by getting involved in some of the educational activities that this department offers.

A moduli space parameterizes certain geometric objects, i.e. the points of the moduli space correspond to isomorphism classes of whatever kind of geometric object you are considering. We'll explore this idea by first looking at the moduli spaces of simple geometric objects such as circles or triangles. We'll work our way up to a (very expository) discussion of the moduli space of curves of genus g, through which we'll see why moduli spaces are interesting and useful.

We will look into the exciting world of topology and explore some of its connections to other fields of mathematics. It is fundamentally connected to almost every part of mathematics but the emphasis of this talk will be on algebraic topology (an interplay between algebra and topology) and in particular on BG theory (the theory of classifying spaces of groups). I will do a survey of results in the subject and explain the project I was working on (if time permits).

Competition between members of the same species is an important factor in the regulation of population growth. Biologists have defined several types of intra-specific competition, such as exploitative, interference, scramble, and contest. Mathematicians then use these definitions to study population growth in the presence of such competition. I will give some examples of scramble and contest competition, and compare their effects on populations using age-structured hierarchical models.

According to Kirillov's idea, the irreducible unitary representations of a Lie group G roughly correspond to the coadjoint orbits of G in the space 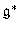dual to the Lie algebra 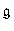of G. Given an integral coadjoint orbit of G, one can apply the method of geometric quantization to construct an unitary representation; on the other hand, by computing a transform of the character of a representation, one can obtain a coadjoint orbit. This method suggests the detailed study of coadjoint orbits, such as, completely classifying coadjoint orbits, finding representatives of orbits, etc.. I will give some elementary background on Lie groups and Lie algebras and briefly describe the method of orbits using examples.

The zeta function of a polynomial equation, or system of equations, over a finite field F, is a formal power series which encodes very compactly a lot of information about solutions in extensions of F. We motivate and define the zeta function, describe the "Weil conjectures" concerning rationality and other properties of the zeta funcion.

Integrability or non-integrability of a system of differential equations is an important but very difficult question. One can compare it to the solvability of a polynomial equation by radicals, but its solution appears more elusive. In this talk I will explain and illustrate Ziglin's theorem which is a very nice sufficient condition for non-integrability of a Hamiltonian system. The Hamiltonian system that I will investigate is of a special form but it is general enough to include many important applications.

Population genetics is a fascinating subject with many obscure applications, as the title suggests. It is also closely connected to mathematics. In my master's thesis, I aim to teach high school students mathematics through population genetics using a series of modules. My talk will be a discussion of this work, and this will be a springboard into methodological and pedagogical issues.

Often a series that diverges by the usual definition may be associated with a value that can reasonably be called its sum. For example, a process due to Euler "sums" the geometric series of any z such that Re(z) < 1 to 1/(1-z). We shall examine various such processes--namely those due to Cesaro and Hoelder, Abel, Euler, and Borel--and then find the general forms of processes that allow for the summation of series. This has applications to the study of Fourier series as well as generalized functions. "Generalized functions" refers to a class of trigonometric series whose members can be treated in some ways as familiar functions even though some are divergent series that are not summable by any of the above processes.

In this talk I will explain why everyone should know number theory.