RECTANGLES - TI 85
Introduction
This program plots the graph of a function f(x), draws
left or right hand rectangles, and computes the corresponding approximation
for 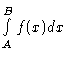 .
.
If you have not used one of the programs posted on this website before,
you should read through
the information in the Intro to Programming
section first.
The Program
| :Prompt A,B,N,T |
{Prompt is in PRGM under I/O} |
| :ClDrw |
{ClDrw is in GRAPH under Draw} |
| :DrawF y1 |
{DrawF is in GRAPH under Draw}
{y1 is found in VARS under EQU} |
| :Pause |
{Pause is in PRGM under CTL} |
:(B-A)/N H H |
{The arrow is in STO} |
:0 S S |
{The 0 is a zero} |
:1 J J |
{The 1 is a one} |
| :Lbl P |
{Lbl is in PRGM under CTL} |
:A+(J-1)*H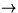 U U |
{The * is the times sign} |
:U+T*H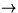 x x |
{x is the x-VAR} |
| :Line(U,0,U,y1) |
{Line is in GRAPH under Draw} {The 0 is a zero}
|
| :Line(U,y1,U+H,y1) |
|
| :Line(U+H,y1,U+H,0) |
|
:S+H*y1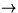 S S |
|
| :IS>(J,N) |
{IS> is in PRGM under CTL} |
| :Goto P |
{Goto is in PRGM under CTL} |
| :Pause |
|
| :Disp "SUM" |
{Disp and " are in PRGM under I/O} |
| :Disp S |
|
Running the Program
You will need to enter a function f(x) into y1 before running
the program. Change the graphing RANGE so that the desired portion of
the function fills the screen. The program will first ask for values of A, B,
and N (number of subdivisions). The value of T determines the type of rectangle
to be viewed. T=0 corresponds to left hand rectangles, T=1 corresponds to
right hand rectangles. Any value between 0 and 1 can also be used.
After plotting the graph, the program will pause. Hit
ENTER. The rectangles will be drawn and the program will pause
again. Hit
ENTER. The value of the approximation will appear.
To test the program try the following:
f(x) = x2+ 3, RANGE:
0< x <5,
0< y <25, A=1, B=4, N=6, T=1.
You should see a portion of a parabola and 6 right hand rectangles.
The numerical answer will be 33.875
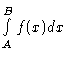 .
.