Rectangles - TI 89 or TI 92

Introduction
This program plots the graph of a function f(x), draws left or right hand rectangles, and computes the corresponding approximation for 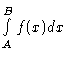$\int\limits_a^bf(x)dx$ .

If you have not used one of the programs posted on this website before, you should read through the information in the Intro to Programming section first.

If you have a TI Connectivity Cable, you can download the program main.rects.89p

The Program

:rects( ) {This will already appear if you named the program rects}

:Prgm {This will already appear}

:Local a,b,n,t {Local is in the F4 menu}

:ClrIO {ClrIO is in the CATALOG menu}

:Input "a=", a {Input is in the F3 menu}

:Input "b=", b

:Input "n=", n

:Input "t=", t

:setMode("Graph","Function")

:ClrDraw {ClrDraw is in the CATALOG menu}

:DrawFunc y1(x) {DrawFunc is in the CATALOG menu} {y1 is the Y followed by a 1}

:(b-a)/n $\to$ h

:0 $\to$ s {The 0 is a zero}

:For j,1,n {For EndFor is in the F2 menu} {The 1 is a one}

:a+(j-1)*h $\to$ u {* is the times button}

:u+t*h $\to$ x

:Line u, 0, u, y1(x) {The 0 is a zero}

:Line u, y1(x), u+h, y1(x)

:Line u+h, y1(x), u+h, 0 {The 0 is a zero}

:s+y1(x)*h $\to$ s

:EndFor

:Pause {Pause is in the CATALOG menu}

:Disp "sum", s {Disp is in the F3 menu}

:EndPrgm {This will already appear}

Running the Program

You will need to enter a function f(x) into y1 before running the program. Change the graphing WINDOW so that the desired portion of the function fills the screen. The program will first ask for values of A, B, and N (number of subdivisions). The value of T determines the type of rectangle to be viewed. T=0 corresponds to left hand rectangles, T=1 corresponds to right hand rectangles. Any value between 0 and 1 can also be used. After plotting the graph, the program will pause. Hit ENTER. The rectangles will be drawn and the program will pause again. Hit ENTER. The value of the approximation will appear.

To test the program try the following:
f(x) = x²+ 3, WINDOW: 0< x <5, 0< y <25, A=1, B=4, N=6, T=1.

You should see a portion of a parabola and 6 right hand rectangles. The numerical answer will be 33.875

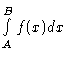:rects( )	{This will already appear if you named the program rects}
:Prgm	{This will already appear}
:Local a,b,n,t	{Local is in the F4 menu}
:ClrIO	{ClrIO is in the CATALOG menu}
:Input "a=", a	{Input is in the F3 menu}
:Input "b=", b
:Input "n=", n
:Input "t=", t
:setMode("Graph","Function")
:ClrDraw	{ClrDraw is in the CATALOG menu}
:DrawFunc y1(x)	{DrawFunc is in the CATALOG menu} {y1 is the Y followed by a 1}
:(b-a)/n $\to$ h
:0 $\to$ s	{The 0 is a zero}
:For j,1,n	{For EndFor is in the F2 menu} {The 1 is a one}
:a+(j-1)*h $\to$ u	{* is the times button}
:u+t*h $\to$ x
:Line u, 0, u, y1(x)	{The 0 is a zero}
:Line u, y1(x), u+h, y1(x)
:Line u+h, y1(x), u+h, 0	{The 0 is a zero}
:s+y1(x)*h $\to$ s
:EndFor
:Pause	{Pause is in the CATALOG menu}
:Disp "sum", s	{Disp is in the F3 menu}
:EndPrgm	{This will already appear}