We all have some idea of infinity () -- of being bigger than any counting number. However, it might seem, upon some reflection, that there are many different infinite sizes.

Consider the set of all counting numbers {1,2,3,...}, and compare it to the set of all even numbers {2,4,6,...}. There are infinitely many of each, and yet it seems obvious that in some sense there are twice as many numbers as even numbers.

Or, consider two concentric circles. Each has infinitely many points on its circumference, yet the outer circle, since it is bigger, seems to contain more points.

Consider the following pairing off of the even numbers with all the counting numbers:

Again, consider our two concentric circles. The circumference of one is longer than that of the other, and so, by straightening them and then lining them up, one can see that the set of points that make up the smaller circle can be paired off with some, but not all, of the points that make up the larger circle.

That may be taken to show that there are more points on the larger circle than on the smaller one. But now, consider a radius which sweeps along our two concentric circles:

Each time it passes through a point on the larger circle, it also passes through a point on the smaller circle. So, the two circles contain the same number of points, even though one is bigger!

Galileo's ideas may be thought to show that all infinite numbers are the same size. That is not correct. Galileo did show that one good way to show that two collections, even two infinite collections, are the same size is to pair them off. He also showed that, strange as it may seem, some infinite collections can be the same size as some of their parts. To show that one infinite collection is really bigger than another, one would have to show that they cannot be paired off.

Georg Cantor managed to show that there actually are infinite sets of different sizes. His simplest argument to that effect is known as the "diagonal" argument. Cantor proved that there are more sets of numbers than there are numbers. Since we can pair off each number with the set whose only member is that number, there cannot be fewer sets of numbers than there are numbers. Suppose there are not more sets of numbers than there are numbers. Then we could pair off the sets with the numbers. Imagine any infinite list of the sets of numbers, in no particular order:

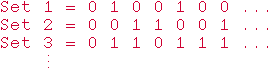
There is a 0 when the corresponding number is not in the set, a 1 when the number is in the set.

Thus, for example, the first set, Set 1, is {2, 5, ...} Now, construct a set as follows: it differs from Set 1 on the first number (and so, since 1 is not in Set 1 it is in the set being constructed), it differs from Set 2 on the second number, it differs from Set 3 on the third number, and so on down the diagonal of the diagram.

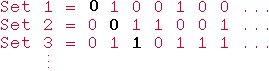
Thus, in our example, the set being constructed includes 1 and 2 but not 3. Since this set differs from the nth set on our list on the nth number, it is not on the list. That is, no infinite list of sets of numbers includes all the sets of numbers. There aren't enough numbers to pair them off with all the sets of numbers. Thus, there are more sets of numbers than there are numbers---some infinities are indeed bigger than others!

(And note that adding the new set to the list won't affect things; we can simply repeat the argument.)

The same basic argument can be used to show something even more fantastic: given any collection, the collection of all of its subsets is bigger than it. Thus, there are more sets of sets of numbers than there are sets of numbers, more sets of sets of sets of numbers than there are sets of sets of numbers, and so on. There are infinitely many infinite sizes.

What's especially interesting to the philosopher is that we can know these facts about the infinite even though we have never encountered an infinite number of things. Rather, it is through the application of reasoning that we have been able to glimpse into the infinite.

For further discussion of the infinite, see Shaughan Lavine (shaughan@ns.arizona.edu), Professor of Philosophy and author of Understanding the Infinite. Courses at The University of Arizona that discuss the infinite include Philosophy 403, 413b, and 416.

Composed by Shaughan Lavine and Dave Truncellito in the UA Department of Philosophy as part of the Math Across the Curriculum group's contribution to Mathematics Awareness Week 1998. Web design by Denice Warren, funded by the NSF Recognition Award for the Integration of Research & Education.