Math410 (Bayly) Homework 3 (due Thursday 22 July)
First of all, read section 6.1 and observe that you did a problem of this type on today’s exam. Next, skim section 6.2 and recognize the material on circuits that we discussed the last couple of days in class. I did not go into as much detail as O&S, and will not discuss some aspects such as “minimum power dissipation”, at least for now.
In section 6.2 I’d like you to turn in 6.2.1 part (e), and not only draw the network but also find the null vectors of the matrix transpose and sketch the corresponding loops in the network. Also do problem 6.2.2. The network does not have nodes labeled, so you may do so any way you like.
Read section 6.3, and realize that things are not as complicated as O&S indicate! If you want complete information about displacements of the ends of beams, you need their formulas, but if you only want the tensions in the beams you only need equation 6.50. I WILL discuss this kind of problem in enough depth so that you understand the fundamentals.
Finally, we are about to begin discussing how to find the “minimum-length” solution when you have a system of equations with an infinite number of solutions. This topic is not discussed until much later in the text, but it’s so elementary that we don’t need the text. Here’s the main idea, in an example with only one free variable:
Suppose the general solution of a system of equations is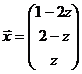 
. The squared length
of this vector is 
. To find the minimum
of this quadratic, use calculus.
Explicitly, we take the derivative 
, and set it to zero: 
, therefore 
minimizes 
. We don’t need to
find the actual minimum value of f,
just the value of z. The corresponding solution vector is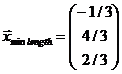
.
As a first exercise in finding minimum-length solutions, I’d
like you to revisit 1.8.2(a) and find its minimum-length solution using
calculus as I did in the preceding paragraph.
Then I’d like you to use the “right pseudoinverse”
technique, in which you calculate the right pseudoinverse
and then get 
. Check that this
answer is the same as the one you got using calculus.
I hope it seems at least somewhat magical that the r.p.i. formula works; I’ll show you later why it
works. I expect you’ll find it pretty
easy to use the formula you memorized for the inverse of a 2x2 matrix. For larger matrices it’s inefficient to
actually find R itself. In practice you would calculate 
first, and then solve 
for 
using Gaussian elimination, and finally set
.
I’ll come up with a couple more minimum-length solution
problems for you tomorrow!