
For the data gathered above, it is seen that 7 out of 24 victims were located during bright, sunny days, while 11 out of 16 were located during overcast days. To estimate the probability of detection (POD) and to test whether these data indicate a statistically significant difference in POD between bright, sunny days and overcast days the following procedure was used. The data gathered during bright, sunny days may be represented as 7 successes in 24 trials of a Bernoulli random variable with unknown parameter ps. In a similar way the data gathered during overcast days may be thought of as 11 successes in 16 trials of a Bernoulli random variable with unknown parameter po, see [3]. The approximate 95% confidence intervals for ps and po are determined such that (see [4], pp 108-117)To test whether ps = po, the UMP (uniformly most powerful unbiased test) is used on the null hypothesis ps = po as described in [3], pp. 141-143. This requires the computation of 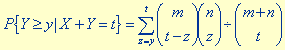
Thus the null hypothesis that ps = po is rejected at a level of .0157, or in everyday language, there is over 98% confidence that the difference is significant.
|