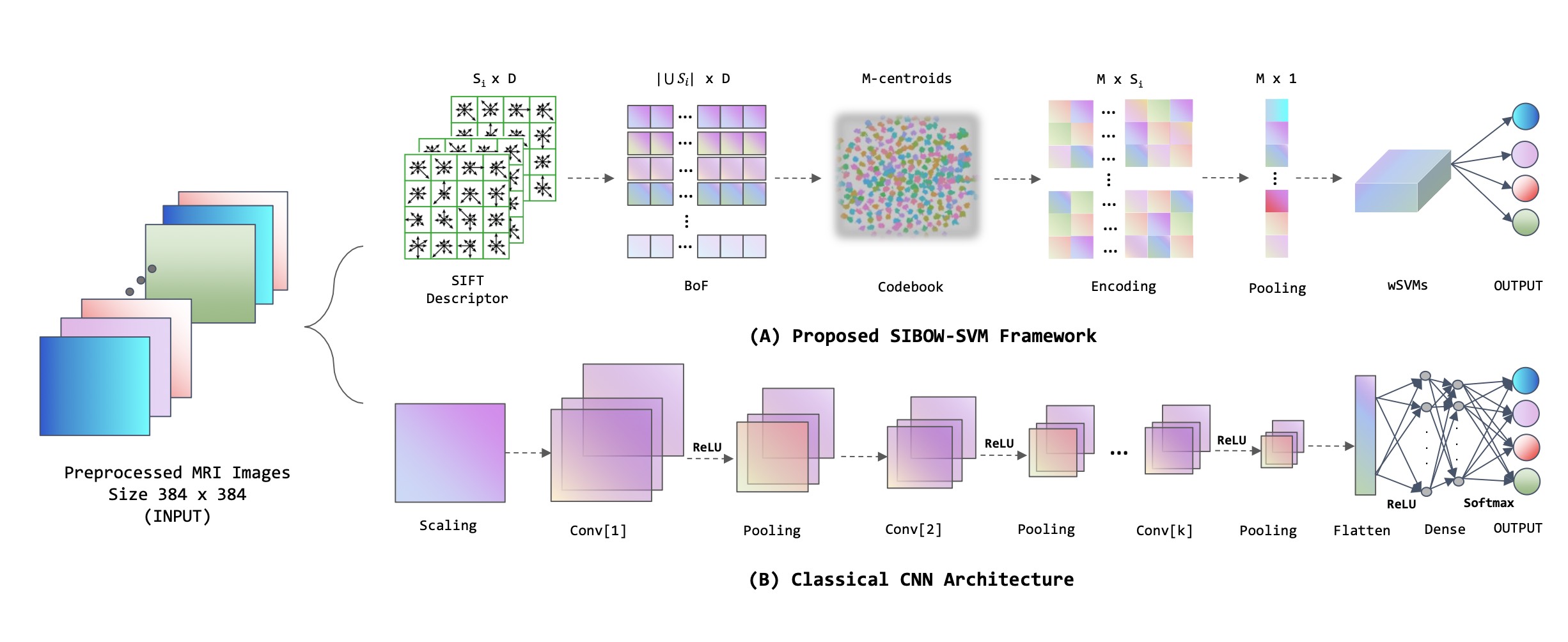
Image source: Robust brain MRI image classification with SIBOW-SVM
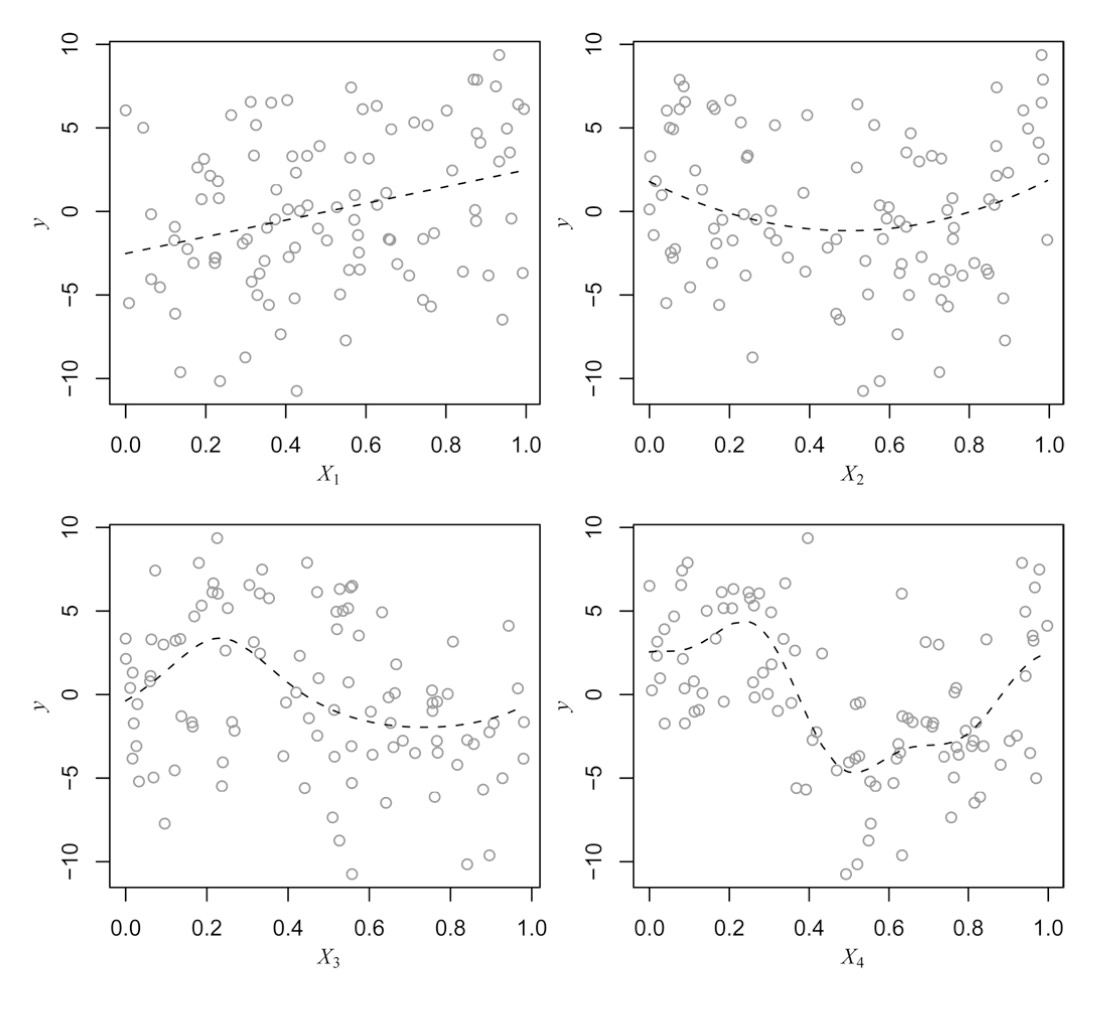
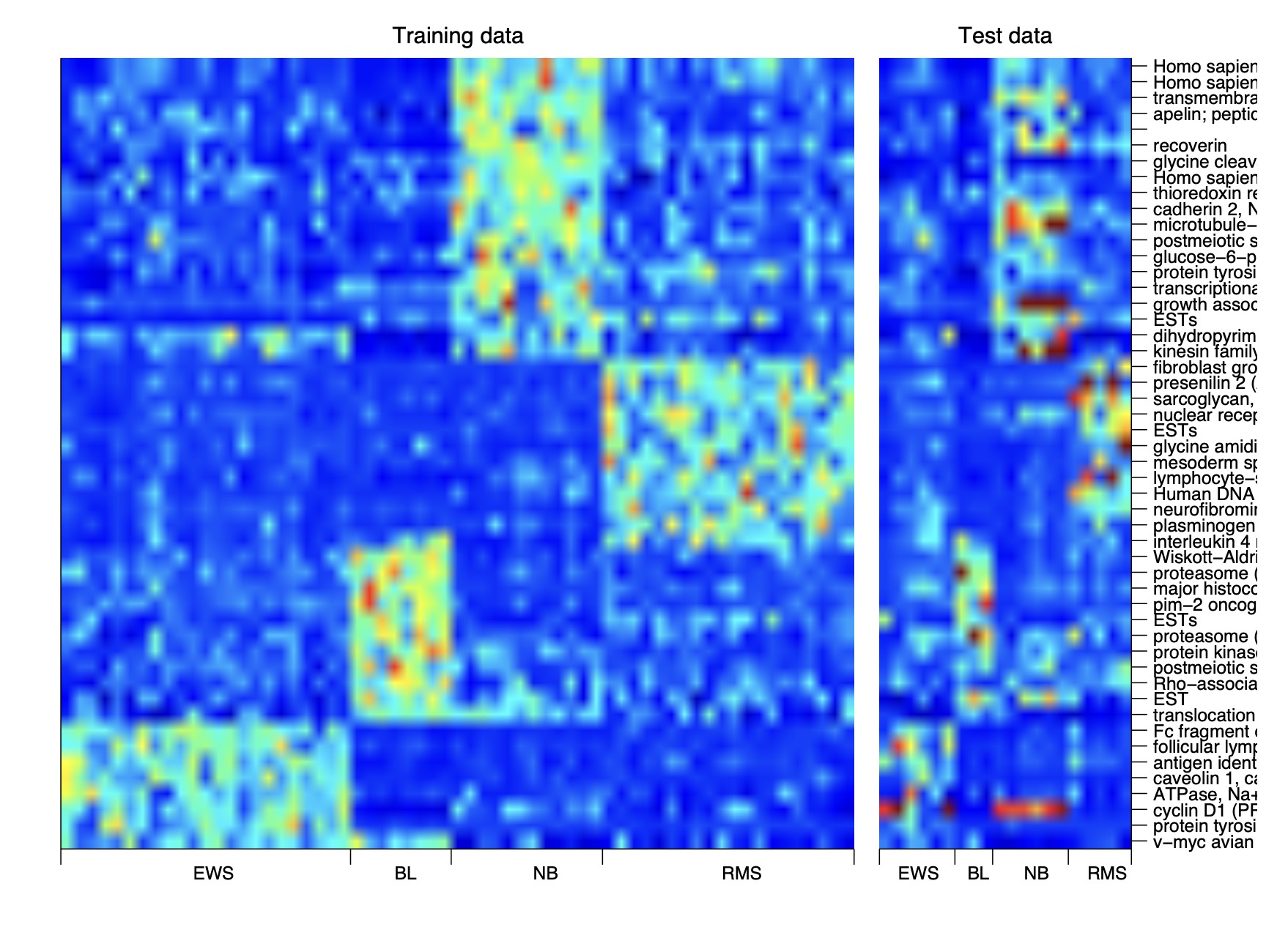
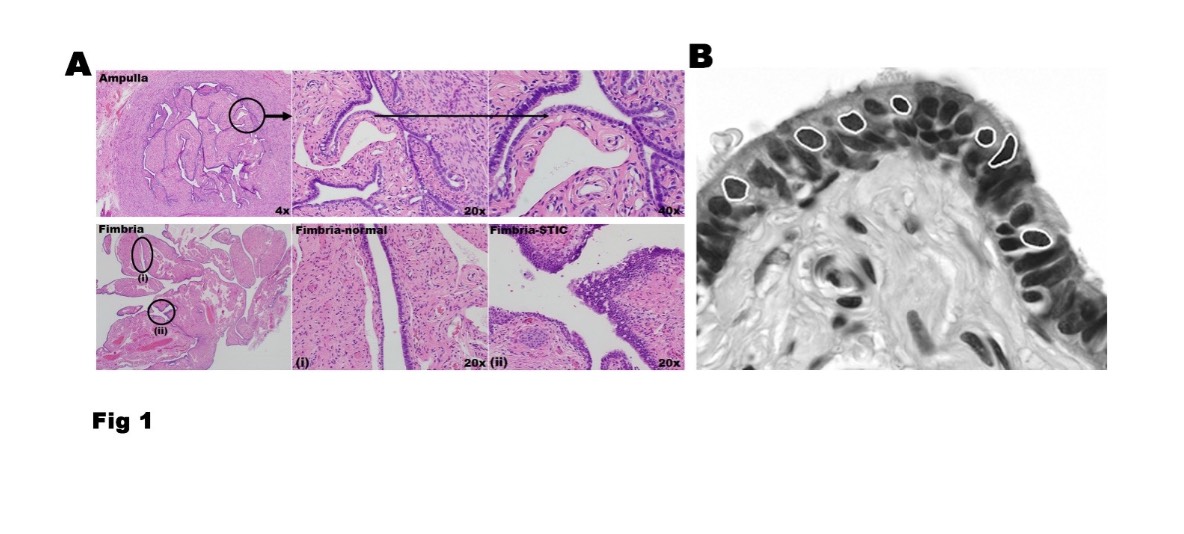
Statistical machine learning combines mathematical learning theory and principles, statistical models, and computing algorithms to learn from data and make decisions. We are particularly interested in supervised learning from complex-structured data with a focus on classification, including unbalanced data, tensor data, image classification, networks, and dynamic problems.
Selected publications in the area
- Zhang, H. H., Liu, Y., Wu, Y. and Zhu, J. (2008) Variable selection for the multicategory SVM via adaptive sup-norm regularization. Electronic Journal of Statistics, 2, 149-167.
- Wu, Y. and Zhang, H. H. (2006) The analysis of rank data using the exponential scoring rule. Statistica Sinica, 16, 1021-1032.
- Zhang, H. H. and Singer, B. (2010) Recursive Partitioning and Applications, Second Edition. Springer, New York.