This program computes left, right, Trapezoid, Midpoint, and Simpson's approximations for
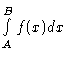 .
.
If you have not used one of the programs posted on this website before, you should read through the information in the Intro to Programming section first.
Introduction
This program computes left, right, Trapezoid, Midpoint, and
Simpson's approximations for
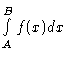 .
.
If you have not used one of the programs posted on this website before,
you should read through
the information in the Intro to Programming
section first.
The Program
| :Prompt A,B,N | {Prompt is in PRGM under I/O} |
| :(B-A)/N |
{The arrow is STO} |
| :A |
{x is x-VAR} |
| :0 |
{The 0 is a zero} |
| :0 |
{The 0 is a zero} |
| :1 |
{The 1 is a one} |
| :Lbl P | {Lbl is in PRGM under CTL} |
| :L+y1*H |
{y1 is in VARS under EQU} {The * is the times sign} |
| :x+H/2 |
|
| :M+y1*H |
|
| :x+H/2 |
|
| :IS>(J,N) | {IS> is in PRGM under CTL} |
| :Goto P | {Goto is in PRGM under CTL} |
| :B |
|
| :L+y1*H |
|
| :A |
|
| :R-y1*H |
|
| :(L+R)/2 |
|
| :(2*M+T)/3 |
|
| :Disp "L R T M S" | {Disp and " are in PRGM under I/O} |
| :Disp L | |
| :Disp R | |
| :Disp T | |
| :Disp M | |
| :Disp S |
Running the Program
You will need to enter a function f(x) into y1 before running
the program. The program will ask for values of A, B, and N (number of
subdivisions).
To test the program try the following:
f(x) = x2+ 3,
A=1, B=4, N=20.
Your answer will be
L R T M S
28.88625
31.13625
30.01125
29.994375
30