Hydrodynamics of Bacterial Colonies

Introduction

Recent experiments [1] with Bacillus subtilis have revealed the existence of large scale motions, which take the form of whirls and jets, and which appear in wet regions of bacterial colonies grown on agar plates. These dynamic behaviors cease to exist if bacteria die or stop swimming, which clearly indicates that they are a consequence of the presence of motile living organisms in the system. Moreover, these motions appear to influence the way the colony grows. As indicated in [1], "whirls and jets frequently strike the boundary at the periphery, become disorganized, and deposit cells there that push the edge of the colony out. Complex colony shape appears to be governed by the locations on the colony boundary where strikes occur and the behavior of the cells remaining at the boundary following the strike".

We developed a hydrodynamic model [2], which describes bacterial dynamics both within and near the boundary of the colony, and which is able to reproduce some of these phenomena. Our simulations of this model [3] made the basis of the cover illustration [4] for the 2007 volume of the journal Nonlinearity.

Hydrodynamic Model

The model described in [2] considers the mixture of bacteria and water as a two-phase fluid and provides a unified framework in which many aspects of colony dynamics may be understood. This model consists of three reaction-diffusion-advection equations for the bacterial density, water density and concentration of nutrients in the medium, coupled to a hydrodynamic equation for the complex fluid made of bacteria and water. These equations are general in the sense that the reaction, diffusion, pressure, stresses and external forcing terms can be chosen differently for different types of microorganisms. They are however tailored to a situation for which bacteria do not emit a chemoattractant and to conditions such that bacterial secretions, waste and pore formation are negligible. Extensions including such phenomena are possible, but are not considered here. Some major characteristics of this model are listed below.

• The model generalizes previous works (see for instance [5-7]) on the description of bacterial colonies in terms of reaction-diffusion equations. Indeed, one can think of our model equations as three coupled reaction-diffusion equations for the bacterial (N), water (W) and nutrient (S) densities, in which the advection terms are prescribed by a velocity field v, which depends on S, N and W through the hydrodynamic equation.
• The hydrodynamic equation contains a pressure term which indicates that bacteria tend to move away from crowded regions. We showed in [2] that if only this term is kept in the right hand side of the hydrodynamic equation, and with specific assumptions regarding the densities of nutrients, bacteria and water, an explicit expression can be found for the velocity field v in terms of S, N and W. In this case, v turns out to be proportional to the gradient of the concentration of nutrients. In this (singular) limit, the model therefore resembles well-known models of reaction-diffusion with chemotaxis, such as the "receptor-law" model [8], or that developed by Keller and Segel [9].
• Finally, the presence of a small-scale (ad-hoc) forcing, which models flagella movement, can lead to the formation of larger-scale vortices and jets. This forcing also provides a source of noise which may in turn facilitate the development of instabilities of the colony boundary and lead to the formation of complex colony shapes.

Phase Diagrams

Colony morphology is often described in terms of phase diagrams, which associate a colony shape to two parameters, namely the initial wetness of the agar W₀, and the initial concentration of nutrients on the plate, S₀. Roughly speaking, a typical phase diagram is devided into two regions, one in which colony growth mostly results from bacterial swimming, and another one in which growth is a consequence of mass increase [10]. The figure below shows a phase diagram obtained from numerical simulations of our model [3], which is in good agreement with experimental observations. Colonies on each row are shown at the same time t, unless otherwise mentioned.

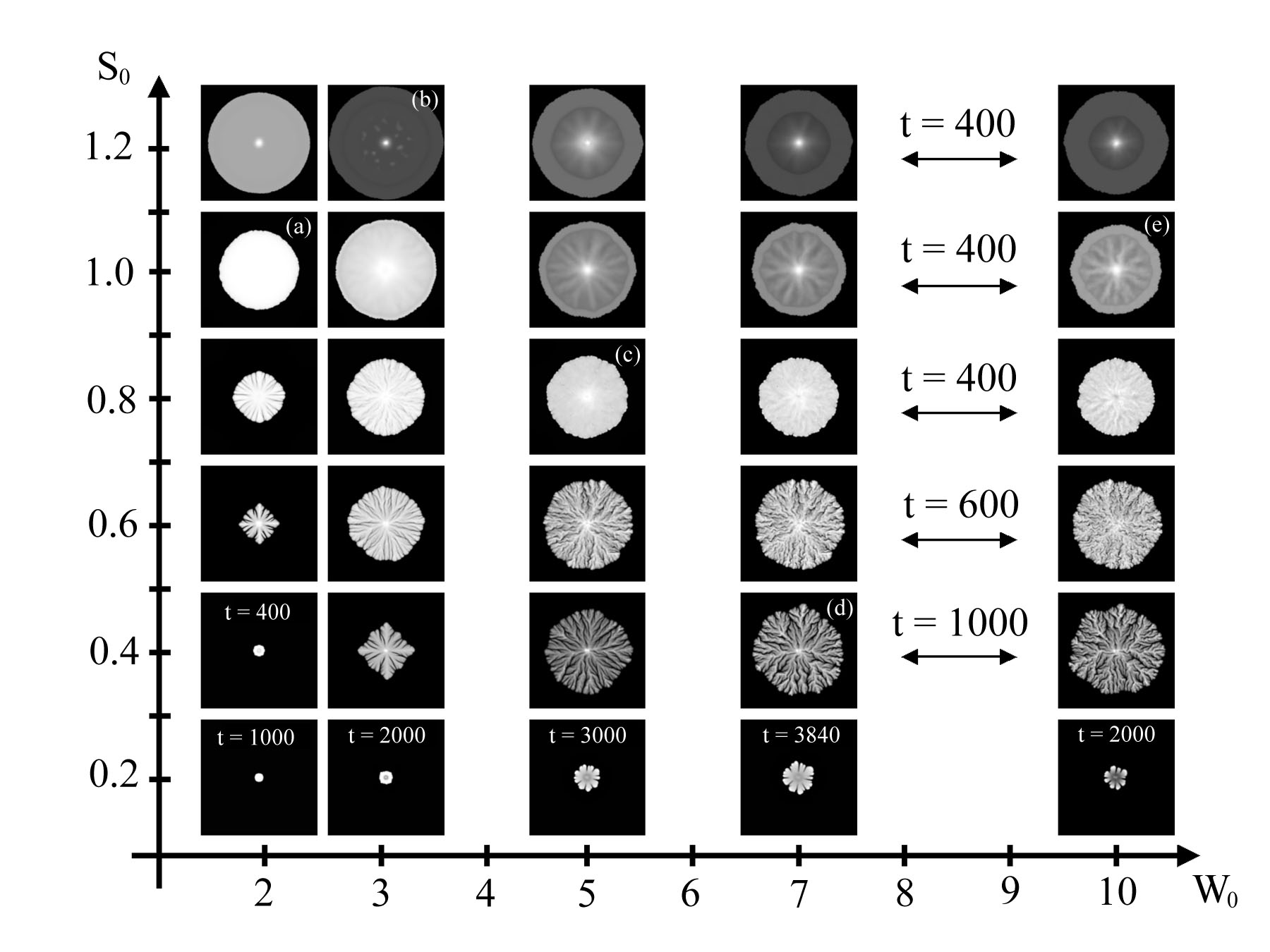
How Dynamic Motions Affect Growth

The first column of the figure below shows cross-sections of N, W and S along a vertical line through the center of the colony, in the cases marked (b) and (d) in the above phase diagram. The second column shows the corresponding two-dimensional velocity fields superimposed on color plots of N. Vectors are plotted every four points and have been rescaled; vectors of magnitude zero are represented by a dot. The third column shows color plots of the vorticity field (vertical component of curl(v)), together with a level curve of N that represents the colony boundary. Note the presence of strong hydrodynamic motions in an anulus near the boudary of the colony marked (b). This is to be contrasted with the case of colony (d), in which hydrodynamic motions are localized at the tips of the colony branches. Also note the presence of spots inside colony (b). These are formed in the later stages of colony development and are due the presence of a velocity field which transports bacteria toward the center of the colony. Further details can be found in [3].

The movies below illustrate some aspects of the growth of these colonies, as described by our model.

• mNR97x_b2.avi (3,174 kB): growth of the colony marked (b) above. Only the first quadrant is shown. The bacterial density is plotted in color, together with the velocity field (arrows). This illustrates the presence of strong hydrodynamic motions in the outer region of the colony.
• mNR97x_b6.avi (2,853 kb): this is an enlargement showing whirls and jets in the outer part of the colony marked (b) above.
• mNR97x_b6_vort.avi (6,611 kb): same as above, but showing the velocity and vorticity fields, together with the colony boundary.
• mR64x_b1.avi (1,614 kB): growth of the colony marked (d) above. Only the first quadrant is shown. The bacterial density is plotted in color, together with the velocity field (arrows). Note that most of the hydrodynamic motions take place at the tips of the colony branches.

Othe movies are also available online from the IOP server.

Online Presentation

A Hydrodynamic Model for the Growth of Bacterial Colonies (from KITP's web site).

Experimental Results

• Movies associated with Reference [1], by N. Mendelson et al.
• Experiments (made by former undergraduate student Cathy Ott, in Professor Mendelson's lab), including a movie showing large-scale bacterial motions in the form of whirls and jets

References

1. N.H. Mendelson, A. Bourque, K. Wilkening, K.R. Anderson & J.C. Watkins, Organized cell swimming motions in Bacillus subtilis colonies: patterns of short-lived whirls and jets, Journal of Bacteriology 181, 600-609 (1999).
2. J. Lega & T. Passot, Hydrodynamics of bacterial colonies: a model, Phys. Rev. E 67, 031906 1-18 (2003).
3. J. Lega & T. Passot, Hydrodynamics of bacterial colonies: phase diagrams, Chaos 14, 562-570 (2004).
4. J. Lega and T. Passot, Hydrodynamics of bacterial colonies, Nonlinearity 20, C1-C6 (2007). (Cover illustration).
5. I. Golding, Y. Kozlovsky, I. Cohen & E. Ben-Jacob, Studies of bacterial branching growth using reaction-diffusion models for colonial development, Physica A 260, 510-554 (1998).
6. M. Mimura, H. Sakaguchi & M. Matsushita, Reaction-diffusion modelling of bacterial colony patterns, Physica A 282, 283-303 (2000).
7. E. Ben-Jacob, I. Cohen & H. Levine, Cooperative self-organization of microorganisms, Advances in Physics, 49, 395-554 (2000).
8. J.D. Murray, Mathematical Biology, Second Edition, Springer-Verlag, Berlin, New York, 1993.
9. E.F. Keller & L.A. Segel, Traveling bands of chemotactic bacteria: a theoretical analysis, J. Theor. Biol. 30, 235-248 (1971).
10. M. Ohgiwari, M. Matsushita & T. Matsuyama, Morphological changes in growth phenomena of bacterial colony patterns, J. Phys. Soc. Jpn. 61, 816-822 (1992).

Acknowledgments

This material is based upon work supported by the National Science Foundation under Grants No DMS9909866 and DMS0075827.
Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.