What follows is a list of some of the projects that faculty members in the department of mathematics have suggested as suitable for undergraduate research projects. Students who wish to participate can register and receive credit for an independent study, or, may be able to get paid to work on these projects (UAMAZ). Details of the requirements will be worked out between the faculty supervisor and the students. Some of these projects require little background and are suitable for freshmen or sophomores, while others require knowledge of linear algebra, ordinary differential equations or group theory. This list is by no means exclusive, any student with a particular interest in some area of research is encouraged to seek out a faculty supervisor, or to come talk with me (Indik) for help on finding a suitable faculty member. Some of the projects that are listed were suggested some time ago, but faculty typically are still willing to work with students on these or a related project.

In addition to contacting the faculty listed with the projects, anyone interested in a research project is encouraged to contact:
Robert Indik Math East 249A indik@math.arizona.edu 621-4599 or
Chris Mikel Math East 146B  mikel@math.arizona.edu 621-2056
Some projects are listed below the table, others are referenced to web pages that are at other locations. If you just print this page, you will not have the full list of projects.
 
 

Ksenija Simic	INTUITIONIST LOGIC (off page)
Arlo Caine	PENROSE TILINGS AND NON-COMMUTATIVE GEOMETRY
Doug Pickrell	SCISSORS CONGRUENCE
Robert Indik	PHASE RECONSTRUCTION FROM NEAR AND FAR FIELD IMAGES
D. E. Myers, R. Harris, M. K. O'Rourke and S. Rogan	USE OF GIS IN ANALYZING ENVIRONMENTAL CANCER RISKS AS A FUNCTION of GEOGRAPHIC SCALE
D. E. Myers	DETECTION OF VEGETATION CHANGE USING NDVI DATA AND SPACE-TIME VARIOGRAMS
Dan Madden and/or William McCallum	MAHLER MEASURES OF POLYNOMIAL OF SMALL DEGREE (off page)
Richard Thompson and Dennis Doxtater	GEOMETRY AND STATISTICS FOR ARCHAEOLOGICAL RESEARCH
Tom Kennedy	SIMULATING SELF AVOIDING RANDOM WALKS (off page)
William McCallum	CONTEMPORARY CRYPTOGRAPHY
T.W. Secomb	MODELING MICROVASCULAR NETWORKS
David Lomen	MATHEMATICAL MODELING
Moysey Brio	SIMULATION OF WAVES AND SHOCKS
Marek Rychlik	INTEGRABLE AND NON-INTEGRABLE BILLIARDS
	SPEECH AND ATTRACTORS
	NEURAL NETWORKS AND GENETIC ALGORITHMS
Joseph Watkins	POPULATION BIOLOGY - modeling and education
Daniel Madden	PATTERNS IN CONTINUED FRACTIONS
Carl Devito	THE NATURE OF TIME AND SPACE

USE OF GIS IN ANALYZING ENVIRONMENTAL CANCER RISKS AS A FUNCTION of GEOGRAPHIC SCALE
Prerequisites: linear algebra, computer experience (word processing, spreadsheet, statistical software or willingness to learn, GIS or willingness to learn), probability theory and statistics desirable.
email: myers@math.arizona.edu telephone 621-6859, Math East 243
The Atlas of Cancer Mortality in the United States: 1950-1994 tabulates the distribution of cancer in the United States by county. The creation and utility of the atlas requires adoption of various assumptions. In particular, it implies that the cancer risk is equal across a county, and that the reported cancer risk represents the cancer risk for all residents of that county. If the county is fairly homogeneous in both the characteristics of the underlying population and exposure risks, then this assumption may be reasonable. However, for many Western U.S. states, this assumption may be inappropriate. These states often are divided into only a few counties, each covering large geographic spaces and having uneven distributions of populations. These characteristics make it unlikely that county-level statistics fairly represent the range of actual county experiences.

The overall goal of this research project, is to examine the geographic variation in the association between cancer risk and arsenic. Arsenic exposure may be a causal agent in the development of bladder, lung, kidney, and skin cancers. Furthermore, arsenic is known to vary across geographic locations. GIS technology has made it more feasible to link multiple sources of descriptive attribute information for various geographic levels with health outcome data.

Several geographically delineated data sets exist in Arizona that allow for exploration of the relationship between arsenic exposure and cancer occurrence. Geocoded cancer incidence and mortality data are available from the Arizona Cancer Registry for bladder, kidney, and lung cancers. Skin cancer data are available from a completed population-based case-control study. Arsenic concentrations are available from a multimedia, multipathway survey conducted in Arizona.

The researchers will examine cumulative, aggregate, and cumulative-aggregate arsenic exposures, as potential doses, with the incidence of specific cancers. They will determine the homogeneity of the associations across various geographic scales.

NDVI data is widely used as an index of vegetation. To detect whether change has occurred in vegetation then it is necessary to detect whether change has occurred in a time sequence of NDVI data files. Because change, if it occurs, may not occur in all parts of a region, i.e., for all pixels in the data sets, some form of statistic is needed that will summarize how the pixel values relate to each other spatially and also temporally. A space-time variogram is one such tool. Then it is necessary to estimate and fit a valid space-time variogram to the data. In this study, data for the years 1990-1999 from the Oregon Pilot Study will be used. The product-sum model variogram not only provides a method for constructing valid space-time variograms but also a way to estimate and fit the model. The characteristics of the fitted model will be interpreted as a tool to ascertain whether there has been a change in the vegetation.

Return to table

Dennis Doxtater and Richard Thompson: Geometry and Statistics for Archaeological Research
Prerequisites: Knowledge of trigonometry, willingness to learn spherical trigonometry and some statistics
Email: doxtater@u.arizona.edu and rbt@math.arizona.edu
Phone: D.D at 621-8130 in College of Architecture, Planning, and Landscape Architecture, and R.T. at 621-2549 in Dept. of Mathematics, room 215.

This is a project outside the math department. Dr. Thompson has helped Dr. Doxtater get started with a project in archeology and an application using the MATHCAD program. A piece of a help wanted description from Dr. Doxtater is included here. Interested students should start by contacting Dr. Thompson.

The effort is to determine whether existing, accurate large-scale geometric patterns between certain archaeological sites and significant natural features are purely coincidental or were designed. I need someone to build a computer application that can run a large number of tests where the location of archaeological sites are randomly varied in relation to fixed natural features. The work can either be for independent academic credit without compensation or funded from grant sources. While the actual test will focus on existing patterns between Anasazi sites in Chaco Canyon and distant mountains and other natural features, the software needs to be generic and usable for other cultural landscapes.

In the Chaco case, there are five distinct geometric patterns that involve both natural and built sites. These five patterns are linked in one way or another through common sites or geometric features. They form a "constellation" with a seemingly logical sequence of linkage and development. In each of the five patterns, it is possible to state the geometric relationship of the archaeological site to natural features as an "angular deviation" (degrees). Thus the accuracy of the overall "constellation" can be defined as the average of the five deviations. The strategy of this introductory research is to calculate the average deviation of randomly located archaeological sites for the particular patterns in a constellation. Conduct this test many times and compare to the average deviation of the existing constellation.

These projects were initially listed by professor Ulmer. Professor McCallum has "taken over" Cryptography (it is a freindly takeover):

Cryptography has probably been with us almost as long as organized military activity, but recently it has become much more important to the public at large. The widespread availability of networked computers and their increasing use in business makes it crucial to be able to communicate securely over unsecure channels. On the other hand, the same widespread availability of powerful computers makes it possible for junior high school students to break, by brute force, codes that would have stoppped the best minds of earlier generations.

One may crudely divide cryptographic systems (codes) into two classes: symmetric key and public key. With symmetric key codes, the parties communicating must share a secret (the "key") in advance and the same key is used for encryption and decryption (hence the label symmetric). These codes typically run fast and are often used for commercial purposes such as bank transfers. Until quite recently, all cryptographic systems were symmetric key systems.

Public key cryptographic systems use different keys for encryption and decryption and, very importantly, knowing one of these keys tells you nothing about the other. Such systems make it possible to perform amazing feats like proving that you know a secret without revealing the secret, or establishing a secret with a stranger using open channels of communication, in such a way that an eavesdropper who hears the entire conversation will not be able to reconstruct the secret.

Here are three possible projects for student research:

• The author of a recent popular book on the history of cryptography is offering a prize of about $15,000 to the first person to decode a certain collection of 10 messages. They are encrypted by 10 different methods, ranging from very simple to very sophisticated. There is a lot to be learned from trying to crack the messages, and you might win quite a lot of money. (But don't count on it to pay your tuition bills!)
• The US government is currently running a competition to select a new (symmetric key) encryption standard to replace the current standard, which is widely used in banking and government business. There are many interesting questions about the various candidates, such as their performance in various implementations and their level of security. The most ambitious question is: "which is best suited to be the new standard?"
• The RSA system is a widely used public key cryptographic system. (For example, it is included in all recent versions of the Netscape web browser.) Its security is based on the difficulty of factoring large integers. Just how secure is this system? More precisely, given current knowledge about algorithms for factoring numbers and current computing power, how long would it take to decrypt a message encrypted with RSA?

Return to table

The microcirculation is an intricate network of tiny blood vessels that carries nutrients to every part of a living tissue. Current projects are aimed at developing mathematical models for several aspects of the system's function. For example, networks continually adjust their structures in response to local signals, during growth and when metabolic requirements change. This process can be modeled using a system of ordinary differential equations to describe changes in vessel diameters. The problem is to determine what types of responses can lead to stable, adequate network structures consistent with experimental observations.

Return to table

David Lomen: MATHEMATICAL MODELING
Prerequisites: varied
email: lomen@math.arizona.edu telephone: 621-6868 room: 602

Topics chosen by the student in areas of mathematical modeling dealing with fluid motion (soil physics, physiology, engineering), with differential equations (pharmacokinetics, biological, chemical, or physical processes,...) or with different ways to teach mathematics or the development of innovative teaching materials.

Return to table

Moysey Brio: SIMULATION OF WAVES AND SHOCKS
Prerequisites: 125b necessary, 223, 215 and 355 useful
email: brio@math.arizona.edu telephone: 621-6864 room: 605

To study various various wave phenomena by running simulations, modifying codes and producing graphics in the study of

• Resonant wave interaction using Fortran software, graphics open
•  Shock-wave interaction, to write Newton's using NAG, graphics open
•  Simulation and detection of heart arrhythmias using Mathematica and Fortran, and or C codes. Also modification of this software for gastro-intestinal modeling.

Marek Rychlik: INTEGRABLE AND NON-INTEGRABLE BILLIARDS
Prerequisites: Basic Calculus sequence, proficiency in a programming language required,
Fourier analysis, probability and linear algebra helpful
email: rychlik@math.arizona.edutelephone: 621-6864 room: 605

Study the motion of a billiard ball on a table of an arbitrary shape. Only elliptic tables are known to be "integrable". Other tables are conjectured to be "chaotic". In the course of this project the student would perform simple numerical experiments to measure the chaotic behavior of tables of various shapes.

Return to table

The student would collect samples of speech, using a computer with a sound card and a microphone. Subsequently, these samples would be visualized, using software like MATLAB. The individual sounds, like the ones produced by saying "aaaah" or "ooooh" produce patterns which are referred to as attractors. These patterns will be subjected to a mathematical analysis to explore the possibility of distinguishing between them.

Return to table

A neural network is a system that will produce ``correct'' responses to a range of inputs. The traditional method of ``training'' of neural networks is the back propagation algorithm and it is known to be very slow. The student will examine a new method of ``genetic breeding'' and compare it to the old method by performing numerical experiments.

Return to table

My recent work involves interaction between the mathematics and biology communities. Under the auspices of the Southwest Regional Institute in the Mathematical Sciences, we are developing ways to communicate research ideas in population biology. This is now being pursued on the biology of bees and soon we will start investigating questions on HIV both its immunology and its epidemiology. Undergraduate projects here come in two types - one is to work with scientists and teachers to develop strategies for communicating these ideas to broad community.

At this moment, we are just starting to write software on bee population models. These models will become tools for high school students, beekeepers and for bee scientists. These groups are concerned about the Africanization of the European honey bee population and mite infestations of bee hives. We hope that these tools will help understand the nature of these events and suggest methods for remediation.

The HIV models will also require some software development. The issues in the immunology are optimal drug protocols for improving the lives of those with HIV. The epidemiological issue is to investigate what changes in behavior will have the biggest impact in the spread of the virus.

Separated from my activities with the Regional Institute, I am also looking into issues involving enzyme kinetics. When the number of enzyme molecules and substrate molecules was high, mass action equations were an adequate mathematical model of the dynamics of the enzyme reactions. As biochemistry is learning more about enzymatic reaction in which the number of molecules is smaller, the stochastic or random effects are playing a more important role. Here we will be writing programs that find the importance of these effects and looking into the experimental data for verification.

Return to table

A continued fraction is a number written in the form:

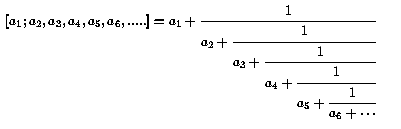
The only numbers that have continued fractions that terminate are the rational numbers. But all numbers, rational and irrational numbers, have unique continued fraction expansions. Some irrational numbers have continued fractions that consist of a repeating pattern of numbers  . We denote these by placing a bar over the repeating part; for example:

These are exactly the irrational numbers that satisfy quadratic polynomials with integer coefficients.

The problem concentrates on the continued fraction expansions of numbers of the form  where n is an integer. These numbers have repeating continued fraction expansions. Some of these expansions can be expressed by a formula that can easily be verified. For example:

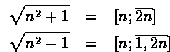
Many such formulae are easy to notice in any good list of expansions. The interesting formulae are those where the number of terms in the repeating pattern grows larger as the number under the square root grows larger. These formulae are harder to pick out and more difficult to verify. The problem is to find, and perhaps verify, formulae for  where the length of the repeating pattern is also a function of n.

This problem requires a certain amount of computer skills, and would require some initial study of continued fractions to get started. The problem is related to a famous open conjectures of Gauss. For example, if one found a formula (highly unlikely) for  where f(x) is a polynomial and where the repeating pattern had length n, this alone would probably prove Gauss' conjecture. To see some of the work that Justin Miller has done click here.

Return to table

At a recent conference here in Tucson researchers in physics and astronomy independently suggested that it may be wise to take a new look at the basic properties of time and space. Innovative mathematical models of time were also presented at the conference and these stimulated some very animated discussions. The project we have in mind is a literature search for papers dealing with unusual observations and/or results dealing with time, and perhaps space as well. Once a body of work is collected, we hope to find clues to unknown, or hidden, aspects of time which may aid in the construction of mathematical models.

Return to table