The dynamics of biological exploitation
xploitation is a broad
term describing the relations of predator to prey,
parasite to host, and herbivore to forage. There is a widespread
acceptance of the importance of exploitation interactions in generating
mammal cycles, but who is the exploiter and who the exploited? Do
the boreal mammal cycles represent an herbivore-carnivore cycle? Is it
the interaction between the herbivore and its food-supply which is central,
with predator populations merely following along? Or are there important
interactions among all three levels, carnivore, herbivore, and vegetation?
One thing is clear: the problem of cyclic fluctuations is fundamentally a problem of dynamics, the change of variables through time. We can explore the dynamics of biological exploitation by modelling the change in populations through time by means of differential equations.
The earliest attempt to capture the dynamics associated with exploitation was that of Vito Volterra, the famous Italian mathematician. Interestingly, at about the same time, Alfred Lotka, the American chemist, studied the same set of equations in the context of a hypothetical chemical reaction. We recall that the Lotka-Volterra equations for the densities P, V of predator and victim species, respectively, read
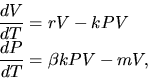
where T is time, r is the victim species' Malthusian rate
of increase, k the per-predator kill rate, 
a conversion factor from victims to baby predators, and m the predator's
death rate.
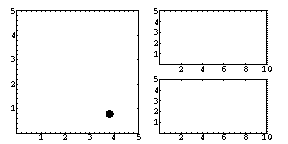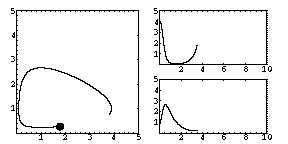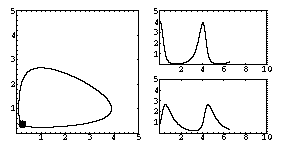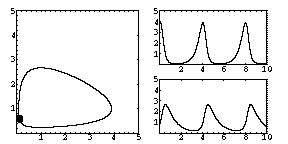As
each of the densities P, V change in time, we can plot each density
against time. The two rightmost graphs show the densities of predator
and victim against time. Which one is which?
We can also plot one density against the other. The resulting graph (on the left) is called a phase portrait. For simple two-variable models such as this, the phase portrait gives us all the essential information about the model.
M & B Home | Previous | Top | Next