Convex Integration

I am interested in the rigidity of underdetermined PDEs, i.e. the global consequences of local differential constraints. An example of this phenomenon is the isometric immersion problem from the previous section.

The isometric immersion problem has an interesting dichotomy depending on the smoothness that we seek for the immersion. Results by Nash, Hartman and Nirenberg and Gromov show that this is a very ``rigid'' problem in low codimension, for C² or smoother immersions. However, for C¹ immersions, the situation is very different. Results due to Nash and Kuiper, along with improvements by Gromov show that

Theorem 5 (Nash-Kuiper-Gromov)   For any C¹ manifold (M^m, g), there is a C¹ isometric immersion $\phi$ : M^m $\rightarrow$ $\mathbb {R}$^m+1. Further, the C¹ isometric immersions of M^m are C⁰ dense in the space of all short immersions $\psi$ : M^m $\rightarrow$ $\mathbb {R}$^m+1.

The proof of this result is through convex integration. Müller and Sverak [MŠ96] adapted this technique to generate Lipschitz solutions u in an admissible set $\mathcal {A}$ that satisfy W(x, u, Du) = 0 a.e., obtaining exact solutions to the (nonregularized) problem (VP). These solutions have an infinite number of scales and are obtained by recursively adding oscillations on increasingly finer scales.

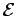
We have used the Nash-Kuiper-Gromov result to show that $\mathcal {E}$^$\epsilon$[u^$\epsilon$] $\rightarrow$ 0 for thin elastic sheets with a variety of boundary conditions, and this can be generalized to the variational problem (R-VP). The proof motivates the following question -

Problem 11   Are the ``convex integration'' solutions relevant to the family of problems (R-VP)? Can one adapt this procedure to include a small scale cutoff?

Also, the convex integration procedure is formulated in spaces with pointwise information on the derivatives (u is Lipschitz or u $\in$ C^k.) To apply this idea to regularized variational problems, we need to consider spaces with integral norms ( $\int_{{\mathcal{S}}}^{}$F < $\infty$, i.e. Sobolev spaces). This leads us to consider questions about the density of smooth (or Lipshitz or continuous) functions in Sobolev spaces of maps between manifolds, e.g.,

Problem 12   What is $\overline{{\{ u \in C^{\infty}({\mathcal S},\Omega), W(x,u,Du) = 0 \mbox{ a.e.}\}}}$ in W^{2, p}($\mathcal {S}$,$\Omega$) ?

This is related to similar questions on Harmonic Maps [EL78,EL88,SU84] and approximation of Sobolev maps between manifolds [Bet90]. It will be very interesting to clarify the role of the geometry of the set {u  |  W(x, u, Du) = 0} in the answer to this question.