


Next: Generalized Crumpling
Up: Research
Previous: Why multiple scale analysis?
Subsections
Nonconvex Variational Problems
A variational problem for a functional
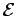 :
: 


 { +
{ +  } is showing the
existence of a minimizer
u*
} is showing the
existence of a minimizer
u* 
 where the infimum of
where the infimum of
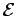 [u] over
u
[u] over
u 
 is attained. Here
is attained. Here
 is the admissible set (usually a subset of an
appropriate function space) and
is the admissible set (usually a subset of an
appropriate function space) and
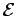 is typically an
integral of a local energy density W(x, u, Du) over the domain
is typically an
integral of a local energy density W(x, u, Du) over the domain
 :
:
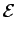 [u] = [u] =  W(x, u, Du)dx. W(x, u, Du)dx. |
(VP) |
A natural approach is to consider a minimizing sequence
uk 
 (a sequence such that
(a sequence such that
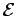 [uk]
[uk] 
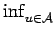
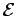 [u]). If
[u]). If
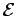 (or
equivalently W) is convex, uk (or a subsequence) converges to a
minimizer u* [Eva98,Dac89]. However, for many
interesting variational problems that arise in physics and geometry,
W is nonconvex. In this case, uk may only converge weakly, and
the variational problem (VP) need not have a
minimizer. Instead, the minimizing sequence might exhibit oscillations
and/or concentration.
(or
equivalently W) is convex, uk (or a subsequence) converges to a
minimizer u* [Eva98,Dac89]. However, for many
interesting variational problems that arise in physics and geometry,
W is nonconvex. In this case, uk may only converge weakly, and
the variational problem (VP) need not have a
minimizer. Instead, the minimizing sequence might exhibit oscillations
and/or concentration.
Models for real physical systems cannot exhibit arbitrarily fine scale
structures. So, we consider the regularized functional
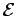
 obtained by perturbing (VP),
obtained by perturbing (VP),
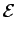  [u] = [u] = 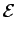 [u] + [u] + 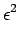  F(x, u, Du, D2u)dx. F(x, u, Du, D2u)dx. |
(R-VP) |
where F is convex in D2u. For
 = 0, we recover the
original functional
= 0, we recover the
original functional
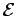 . For any nonzero
. For any nonzero  however, the second term penalizes structures on very fine
scales. This effectively introduces a small scale cutoff and
regularizes the original nonconvex variational problem
(VP). For every
however, the second term penalizes structures on very fine
scales. This effectively introduces a small scale cutoff and
regularizes the original nonconvex variational problem
(VP). For every

 0,
0,
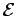
 has a minimizer
u
has a minimizer
u . The following questions arise in
studying the
. The following questions arise in
studying the

 0 limit of the problems
(R-VP):
0 limit of the problems
(R-VP):
 Morphology
Morphology
- Do the minimizers
u
 display oscillations or concentration effects?
Describe the oscillatory/singular regions in the solutions.
display oscillations or concentration effects?
Describe the oscillatory/singular regions in the solutions.
 Scaling
Scaling
- How do
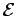
 (u
(u ), and the length scales associated
with the oscillations/singular regions in the minimizer
u
), and the length scales associated
with the oscillations/singular regions in the minimizer
u depend on
depend on  ?
?
 Variational Convergence
Variational Convergence
- Does
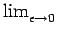 u
u exist, in some appropriate sense? If so, is it possible
to define a suitable limiting process for the energy functionals, so
that
exist, in some appropriate sense? If so, is it possible
to define a suitable limiting process for the energy functionals, so
that
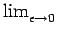
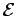


 , implies that
, implies that
 has a minimizer
has a minimizer
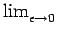 u
u ?
?
The answers to these questions depend on the precise functional forms
of W and F. As

 0, we expect that
Du
0, we expect that
Du converges to K, the zero set of W(.) in some
fashion. In particular we are looking for gradients v = Du such that
v
converges to K, the zero set of W(.) in some
fashion. In particular we are looking for gradients v = Du such that
v  K. Whether such gradient fields v exist depend on a subtle
interplay between the differential constraint Dv = DvT and the
geometry of K.
K. Whether such gradient fields v exist depend on a subtle
interplay between the differential constraint Dv = DvT and the
geometry of K.
If we ignore the fact that v is a gradient, Eq. (R-VP) is
related to the harmonic map
v : 
 K, given by
minimizing
K, given by
minimizing
 F(v, Dv)dx. The variational problem (R-VP)
can thus be interpreted as a Harmonic map problem with an additional
differential constraint. The variational problem for (R-VP) is
also related to the recent work by Müller and Sverák on
obtaining counterexamples to regularity using convex
integration.
F(v, Dv)dx. The variational problem (R-VP)
can thus be interpreted as a Harmonic map problem with an additional
differential constraint. The variational problem for (R-VP) is
also related to the recent work by Müller and Sverák on
obtaining counterexamples to regularity using convex
integration.
Another motivation for this study is condensed matter physics. I am
interested in the general principles that underlie the spontaneous
formation of structures in the minimizers for variational problems.
Many physical systems are governed by the minimization of an
appropriate free energy. This energy usually has many scales
reflecting the multiplicity of the relevant physical processes. Energy
minimization can then lead to a variety of multiple scale structures
including point and line singularities (vortices), microstructure,
domain wall branching and multiple scale oscillations, and this
behavior can be analyzed through the model problem (R-VP).
Energy Concentration and Minimal Obstructions
Consider energy functionals of the type
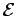
 =
=  Wdx +
Wdx + 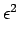
 Fdx. We will assume that W is
nonconvex, F is convex in a higher order derivative,
W, F
Fdx. We will assume that W is
nonconvex, F is convex in a higher order derivative,
W, F  0
by definition and
0
by definition and
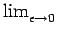
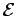
 (u
(u ) = 0. These assumptions are satisfied, for
instance, by the generalized crumpling
problem.
) = 0. These assumptions are satisfied, for
instance, by the generalized crumpling
problem.
If  is small, then W for the minimizer
u
is small, then W for the minimizer
u , is
small over a large part of the domain. This motivates the
consideration of the set
, is
small over a large part of the domain. This motivates the
consideration of the set
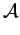
' =
 u
u 
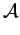
,
 Fdx
Fdx <
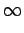
and
W = 0 a.e.
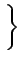
.
Conjecture 1
If
 '
' 
 , then, as
, then, as

 0,
the solutions
u
0,
the solutions
u converge to the minimizer of the convex
variational problem - Minimize
converge to the minimizer of the convex
variational problem - Minimize  Fdx for
u
Fdx for
u 
 '.
'.
If
 ' =
' =  and the minimizing sequence
u
and the minimizing sequence
u does not contain fine scale oscillations, then
u
does not contain fine scale oscillations, then
u and some of its derivatives still converge pointwise
a.e. to the set W = 0. However, there is now an exceptional set of
points, the singular set
and some of its derivatives still converge pointwise
a.e. to the set W = 0. However, there is now an exceptional set of
points, the singular set
 , where some of the
higher derivatives diverge in a manner such that
for any open set
O
, where some of the
higher derivatives diverge in a manner such that
for any open set
O 
 . This leads to energy
concentration on the set
. This leads to energy
concentration on the set
 as
as

 0. Since points in
0. Since points in
 -
-  are regular, the
previous argument restricted to
are regular, the
previous argument restricted to
 -
-  gives
We define
gives
We define
 to be a minimal obstruction, if
to be a minimal obstruction, if
 'loc(
'loc( )
) 
 , and no proper
subset of
, and no proper
subset of
 has this property. These arguments suggest
the following conjecture :
has this property. These arguments suggest
the following conjecture :
Conjecture 2
The minimizing sequence does not have
oscillations/concentration effects iff
 ' is
nonempty. Also, if
' is
nonempty. Also, if
 ' =
' =  and the minimizing
sequence does not have oscillations, the energy concentrates on a
(finite union of) minimal obstruction(s).
and the minimizing
sequence does not have oscillations, the energy concentrates on a
(finite union of) minimal obstruction(s).
This conjecture addresses the issue of Morphology
in the list above. It also relates analytical questions about the
family of variational problems (R-VP) to geometric/topological questions about the set of
functions
{u | W = 0, Fdx <
Fdx <  }.
}.



Next: Generalized Crumpling
Up: Research
Previous: Why multiple scale analysis?
Shankar
2003-11-29
![]() :
: ![]()
![]()
![]()
![]() { +
{ + ![]() } is showing the
existence of a minimizer
u*
} is showing the
existence of a minimizer
u* ![]()
![]() where the infimum of
where the infimum of
![]() [u] over
u
[u] over
u ![]()
![]() is attained. Here
is attained. Here
![]() is the admissible set (usually a subset of an
appropriate function space) and
is the admissible set (usually a subset of an
appropriate function space) and
![]() is typically an
integral of a local energy density W(x, u, Du) over the domain
is typically an
integral of a local energy density W(x, u, Du) over the domain
![]() :
:
![]()
![]() obtained by perturbing (VP),
obtained by perturbing (VP),
![]()
![]() K, given by
minimizing
K, given by
minimizing
![]() F(v, Dv)dx. The variational problem (R-VP)
can thus be interpreted as a Harmonic map problem with an additional
differential constraint. The variational problem for (R-VP) is
also related to the recent work by Müller and Sverák on
obtaining counterexamples to regularity using convex
integration.
F(v, Dv)dx. The variational problem (R-VP)
can thus be interpreted as a Harmonic map problem with an additional
differential constraint. The variational problem for (R-VP) is
also related to the recent work by Müller and Sverák on
obtaining counterexamples to regularity using convex
integration.
![]()
![]() =
= ![]() Wdx +
Wdx + ![]()
![]() Fdx. We will assume that W is
nonconvex, F is convex in a higher order derivative,
W, F
Fdx. We will assume that W is
nonconvex, F is convex in a higher order derivative,
W, F ![]() 0
by definition and
0
by definition and
![]()
![]()
![]() (u
(u![]() ) = 0. These assumptions are satisfied, for
instance, by the generalized crumpling
problem.
) = 0. These assumptions are satisfied, for
instance, by the generalized crumpling
problem.
![]() is small, then W for the minimizer
u
is small, then W for the minimizer
u![]() , is
small over a large part of the domain. This motivates the
consideration of the set
, is
small over a large part of the domain. This motivates the
consideration of the set