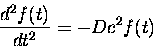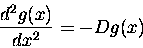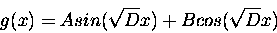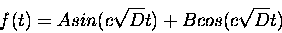|

Solving Linear ODE
We now want to solve the ODEs that we got by
simplifying the wave equation:
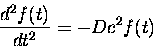
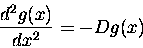 As you see, the two equations are very similar, except that one
involves a function of time and the other involves a
function of space, so we only need to solve one equation, and
the other one will have the same solution. This type of linear
ODE is usually solved by trigonomoteric substituion - assume
that g(x) = Asin (kx) +Bcos(kx) and determine what k must be.
Notice that we have two arbitrary constants A and B, which
appear because we lose constants when we
take derivatives, so in an equation with two derivatives there
are always two arbitrary constants. We need additional
conditions on the function in order to solve the equation completely,
and we will do this in step 3.
Now that we have a guess, we need to show that it actually satisfies
the equation. Taking the second derivative of Asin(kx) and Bcos(kx)
results in the same function, only multiplied by -k^2. So we can
write the equation now in terms of our sines and cosines:
-k^2(A sin(kx) + B cos (kx)) = -D(Asin(kx) + B cos (kx))
It is clear that in order for this equation to be true,
k^2 must equal D. Now that we know k, we have the solution to
this ODE (with some undetermined constants, still):
As you see, the two equations are very similar, except that one
involves a function of time and the other involves a
function of space, so we only need to solve one equation, and
the other one will have the same solution. This type of linear
ODE is usually solved by trigonomoteric substituion - assume
that g(x) = Asin (kx) +Bcos(kx) and determine what k must be.
Notice that we have two arbitrary constants A and B, which
appear because we lose constants when we
take derivatives, so in an equation with two derivatives there
are always two arbitrary constants. We need additional
conditions on the function in order to solve the equation completely,
and we will do this in step 3.
Now that we have a guess, we need to show that it actually satisfies
the equation. Taking the second derivative of Asin(kx) and Bcos(kx)
results in the same function, only multiplied by -k^2. So we can
write the equation now in terms of our sines and cosines:
-k^2(A sin(kx) + B cos (kx)) = -D(Asin(kx) + B cos (kx))
It is clear that in order for this equation to be true,
k^2 must equal D. Now that we know k, we have the solution to
this ODE (with some undetermined constants, still):
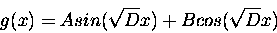 By essentially the same process, we determine that
the solution to the time equation is:
By essentially the same process, we determine that
the solution to the time equation is:
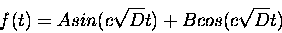
| BACK |
|
|