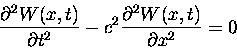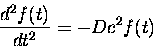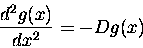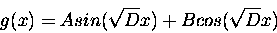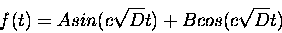|
Periodic FunctionsYou may have noticed the common mathematical thread which runs through all blood-flow related phenomena: they all repeat over and over. The heart goes through its cycle of contraction and relaxation (called a systole), performing the same proccess 70 times a minute. Pressure also goes up and down repeatedly, and so does blood flow - when the heart contracts, pressure rises, when the heart relaxes (for a split second) the pressure drops. This behavior is known as periodic, and mathematicians have special functions that describe this behavior - they are sines and cosines that we learn in trigonometry (see figure). 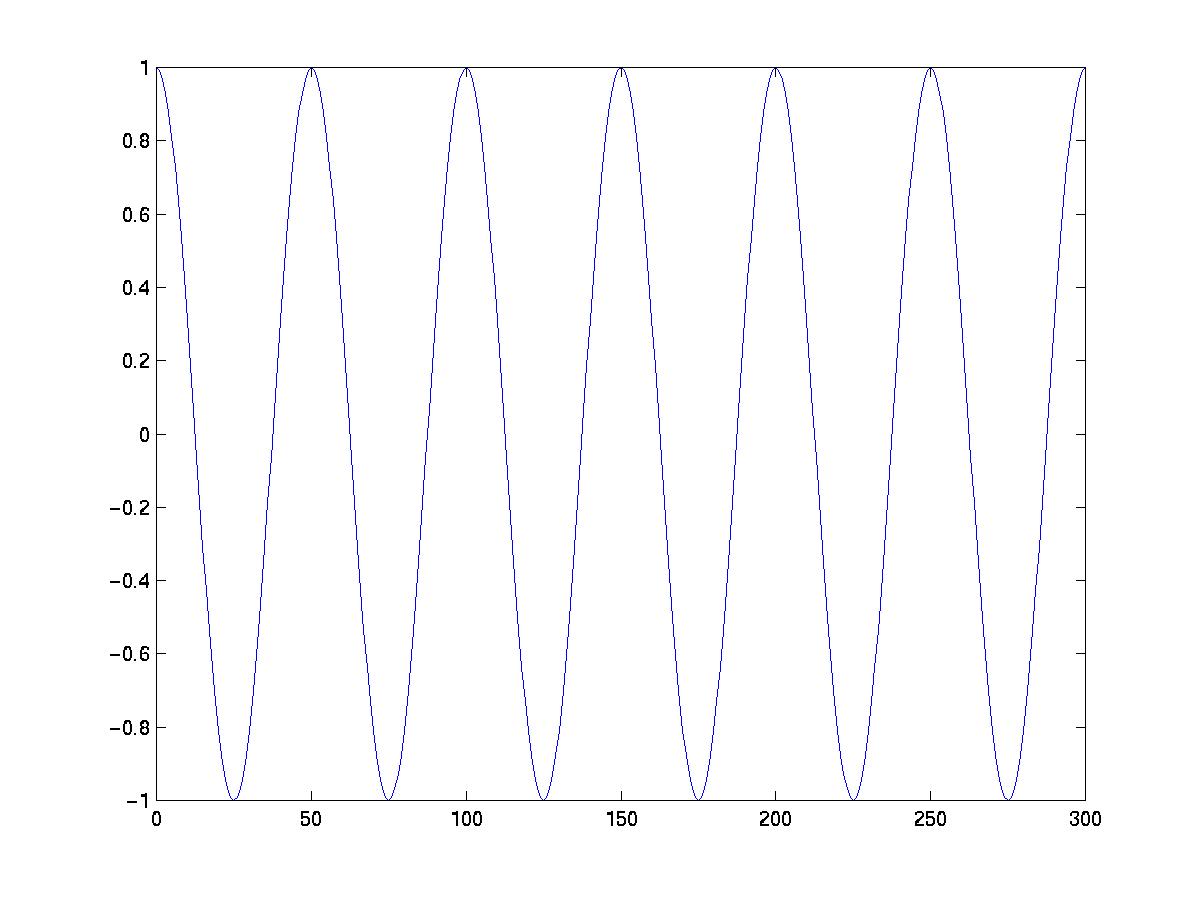
In fact, blood flows through arteries, very much like a sine wave, where the amplitude is the maximum blood flow, and the frequency is the heart rate. There is a beatiful partial differential equation known as the wave equation, which describes an idelized wave, be it ocean waves, blood flowing periodically, or ripples spreading in a pond from the place where you dropped a pebble.
We would like to find solutions of the wave equation that we see in nature - the sine and cosine waves. Below I will outline the steps that are necessary to solve this old chestnut, and for more details, just click on the links.
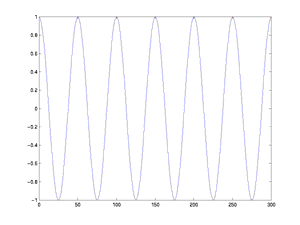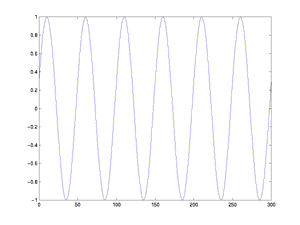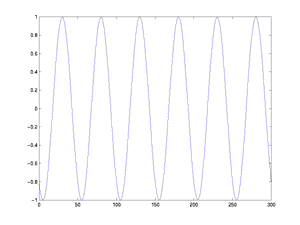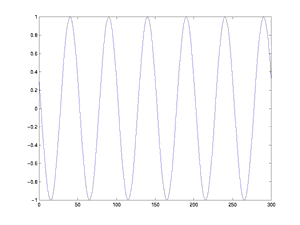
 This function is a reasonably realistic model for blood flow in the
arteries (not the capillaries, though). Notice that the frequency
in time is ten times the frequency in space, which corresponds
to our chosen speed of propagation of 10 cm/sec. The solution is the
cosine wave in space that moves through time, like this:
This function is a reasonably realistic model for blood flow in the
arteries (not the capillaries, though). Notice that the frequency
in time is ten times the frequency in space, which corresponds
to our chosen speed of propagation of 10 cm/sec. The solution is the
cosine wave in space that moves through time, like this:
|