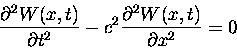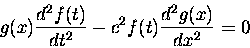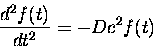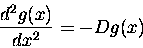Separation of Variables

Our goal is to solve the wave equation, which is of the form:

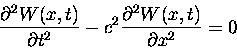
Let us assume that the solution can be written as a product of a function of time (t) and a function of space (x). W(x,t) = f(t)g(x). Then we can easily recompute the partials and re-write the wave equation like this:

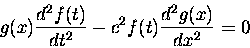Let us now divide everything by f(t)g(x). We now get this:

We see that we have two terms, where one depends only on x, and the other depends only on t. Since the equation has to be true at all times and at any point in space, we conclude that these two terms are constant (let's call this constant -D) - otherwise we could vary time and change the first term, but the second term would not change if we didn't change x, and then the two terms would not add up to zero. So from this we get two equations, which are now ordinary differential equations because each depends only on one variable:

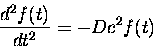
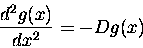
| BACK |