

Next: Invariant theory
Up: Research Statement
Previous: Research Interests
Subsections
My dissertation research
The subject of my dissertation is the bifurcation problem for reversible dynamical systems and a specific application to the elliptical instability for fluid flows.
A system of differential equations
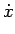 = F(x, t), x = F(x, t), x 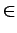 V V |
(1) |
is said to be reversible with respect to a linear involution
R : V 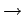 V if and only if
V if and only if
RF(x, t) = - F(Rx, - t).
Similarly, the system
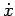 = F(x, t) is symmetric
with respect to a linear operator
S : V
= F(x, t) is symmetric
with respect to a linear operator
S : V 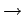 V if
SF(x, t) = F(Sx, t).
V if
SF(x, t) = F(Sx, t).
We investigate normal forms of system (1) at critical
points. The normal forms are the ``simplest'' representation of
Eq(1), consisting of those terms of the Taylor polynomial that
cannot be eliminated via a series of near identity non-linear change
of coordinates.
Linear Problem
In Eq(1), when
V = 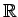 n, F is autonomous and
F(0) = 0, we obtain
n, F is autonomous and
F(0) = 0, we obtain
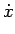
=
Lx +
N(
x),
where L = DF(0). Reversibility implies LR = - RL. This means if 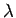 is
an eigenvalue of L, so are -
is
an eigenvalue of L, so are - 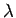 and
and
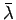 . We
consider cases where all eigenvalues have zero real parts.
. We
consider cases where all eigenvalues have zero real parts.
We first show that L and the corresponding reversing matrix R
can be simultaneously brought to their convenient ``standard'' forms,
by a similarity transformation. Also see [Sev92]. We shall
refer to the ``standard'' form of L at criticality as L0.
Sevyruk's calculation on the versal deformations of reversible
matrices [Sev92] allows us to compute the codimension of any
reversible matrix L0. We identify 3 codimension one cases and 6
codimension two cases.
The Nonlinear Problem
The nonlinear part N of the normal form is completely characterized
by the homological equation:
| DxN(x) . L0*x - L0*N(x) = 0. |
(2) |
This first order system of PDEs can be solved by the
method of characteristics. However, we are not looking for the unique
solution of an initial value problem. Instead, we are interested in
finding polynomial solutions (in x) for N(x) [ETB+88].
Associated with Eq. (2) is the scalar differential equation:
This differential equation has the same base characteristic system as
Eq(2). We seek a general solution
G(x) 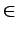 {u} where
{u} are all first integrals polynomial in x. Let
{uB} be a minimal subset of {u} such that every u can be
written as a polynomial in {uB}. The task is to decide whether a
finite set {uB} exists and if it does, to compute it. Also, can
we obtain a unique representation for {u} and if so, how? We will
consider these questions in section 3.
{u} where
{u} are all first integrals polynomial in x. Let
{uB} be a minimal subset of {u} such that every u can be
written as a polynomial in {uB}. The task is to decide whether a
finite set {uB} exists and if it does, to compute it. Also, can
we obtain a unique representation for {u} and if so, how? We will
consider these questions in section 3.
We construct from this G the description for the
normal form N(x). We then apply the reversing symmetries to the
normal forms for further simplification. These normal forms contain
unspecified coefficients that can be determined for specific cases, in
particular, for the elliptical instability problem.


Next: Invariant theory
Up: Research Statement
Previous: Research Interests
May