MATLAB GUIs

Partial Differential Equations

Vibrating String

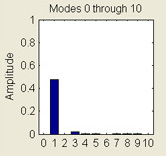
This MATLAB GUI illustrates the use of Fourier series to simulate the dynamics of a vibrating string. The string is clamped at its end points and its deflection from the horizontal, u, evolves according to the wave equation, u_tt - u_xx = 0.

Rectangular Elastic Membrane

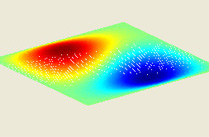
This MATLAB GUI illustrates how the vibrating modes of a rectangular membrane evolve in time and interact with one another. The membrane is clamped at its boundary and its deflection from the horizontal, u, evolves according to the two-dimensional wave equation, u_tt = c²(u_xx + u_yy).

Circular Elastic Membrane

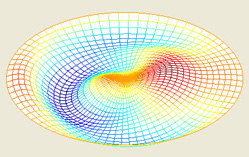
This MATLAB GUI illustrates how the vibrating modes of a circular membrane evolve in time and interact with one another. The membrane is clamped at its boundary and its deflection from the horizontal, u, evolves according to the two-dimensional wave equation, u_tt = ∇²u.

One-dimensional Heat Equation

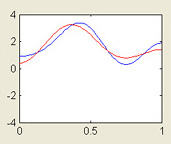
This MATLAB GUI illustrates the use of Fourier series to simulate the diffusion of heat in a domain of finite size. The quantity u evolves according to the heat equation, u_t - u_xx = 0, and may satisfy Dirichlet, Neumann, or mixed boundary conditions.

Heat Equation on the Whole Line

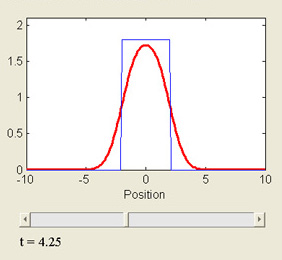
This MATLAB GUI plots the solution to the one-dimensional heat equation, u_t = c²u_xx, as a function of time and for "top hat" initial conditions.