Math 322 - Mathematical Analysis for Engineers
Sturm-Liouville Eigenfunctions
This MATLAB GUI explores the orthogonality properties of several families of Sturm-Liouville eigenfunctions and emphasizes the geometric significance of the orthogonality relationship between two (different) eigenfunctions in the same family.
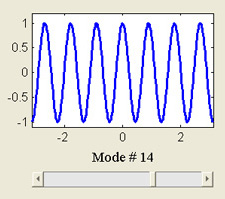
Vibrating String
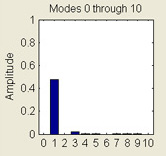
This MATLAB GUI illustrates the use of Fourier series to simulate the dynamics of a vibrating string. The string is clamped at its end points and its deflection from the horizontal, u, evolves according to the wave equation, utt - uxx = 0.
Circular Elastic Membrane
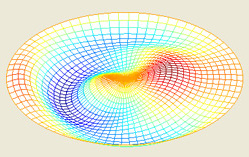
This MATLAB GUI illustrates how the vibrating modes of a circular membrane evolve in time and interact with one another. The membrane is clamped at its boundary and its deflection from the horizontal, u, evolves according to the two-dimensional wave equation, utt = ∇2u.
Rectangular Elastic Membrane
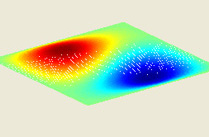
This MATLAB GUI illustrates how the vibrating modes of a rectangular membrane evolve in time and interact with one another. The membrane is clamped at its boundary and its deflection from the horizontal, u, evolves according to the two-dimensional wave equation, utt = c2(uxx + uyy).
One-dimensional Heat Equation
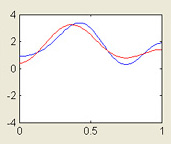
This MATLAB GUI illustrates the use of Fourier series to simulate the diffusion of heat in a domain of finite size. The quantity u evolves according to the heat equation, ut - uxx = 0, and may satisfy Dirichlet, Neumann, or mixed boundary conditions.
Heat Equation on the Whole Line
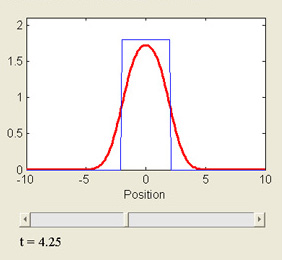
This MATLAB GUI plots the solution to the one-dimensional heat equation, ut = c2uxx, as a function of time and for "top hat" initial conditions.
Mass-Spring System
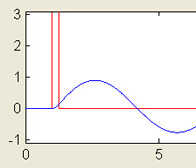
This MATLAB GUI simulates the solution to the ordinary differential equation m y'' + c y' + k y = F(t), describing the response of a one-dimensional mass spring system with forcing function F(t) given by (i) a unit square wave or (ii) a Dirac delta function (e.g. "hammerblow"). Without loss of generality, m is set to 1.