All available GUIs
Circular Elastic Membrane
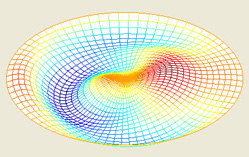
This MATLAB GUI illustrates how the vibrating modes of a circular membrane evolve in time and interact with one another. The membrane is clamped at its boundary and its deflection from the horizontal, u, evolves according to the two-dimensional wave equation, utt = ∇2u.
Diffusion at the Microscopic Level
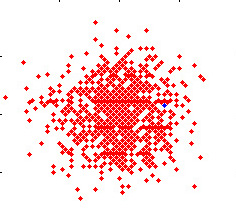
This MATLAB GUI simulates the random motion of M non-interacting particles on a grid. Each particle can only go up, down, left or right, with equal probability. All of the particles start their random walk from the origin, at the center of the box.
Heat Equation on the Whole Line
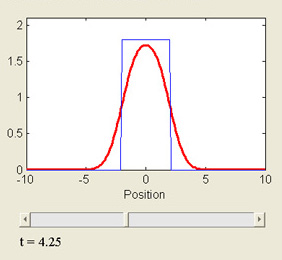
This MATLAB GUI plots the solution to the one-dimensional heat equation, ut = c2uxx, as a function of time and for "top hat" initial conditions.
Julia Sets
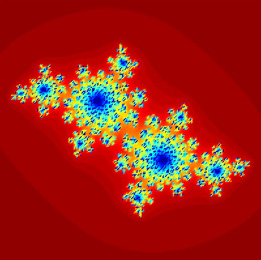
This MATLAB GUI iterates the quadratic map f(z) = z2+ c, where z and c are complex numbers. The (filled in) Julia set is the set of initial conditions z0 such that successive iterates z1 = f(z0), z2 = f(z1), ..., zn+1 = f(zn), ... remain bounded.
Mass-Spring System
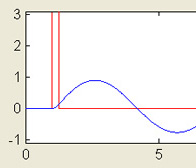
This MATLAB GUI simulates the solution to the ordinary differential equation m y'' + c y' + k y = F(t), describing the response of a one-dimensional mass spring system with forcing function F(t) given by (i) a unit square wave or (ii) a Dirac delta function (e.g. "hammerblow'). Without loss of generality, m is set to 1.
One-dimensional Heat Equation
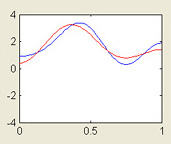
This MATLAB GUI illustrates the use of Fourier series to simulate the diffusion of heat in a domain of finite size. The quantity u evolves according to the heat equation, ut - uxx = 0, and may satisfy Dirichlet, Neumann, or mixed boundary conditions.
Simple Plotter
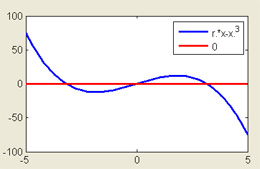
This MATLAB GUI provides a simple way of visualizing bifurcation diagrams by plotting functions that depend on a single control parameter. One of the functions could for instance be the right-hand side of the normal form of a standard codimension-one bifurcation, and the second function could be equal to zero.
Rectangular Elastic Membrane
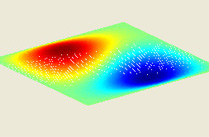
This MATLAB GUI illustrates how the vibrating modes of a rectangular membrane evolve in time and interact with one another. The membrane is clamped at its boundary and its deflection from the horizontal, u, evolves according to the two-dimensional wave equation, utt = c2(uxx + uyy).
Sea Shells

This MATLAB GUI plots a variety of sea shells defined as parametric surfaces. An explanation of the significance of the various parameters may be downloaded from this web site.
Sturm-Liouville Eigenfunctions
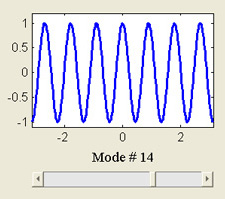
This MATLAB GUI explores the orthogonality properties of several families of Sturm-Liouville eigenfunctions and emphasizes the geometric significance of the orthogonality relationship between two (different) eigenfunctions in the same family.
Vibrating String
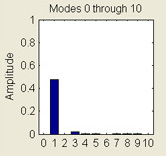
This MATLAB GUI illustrates the use of Fourier series to simulate the dynamics of a vibrating string. The string is clamped at its end points and its deflection from the horizontal, u, evolves according to the wave equation, utt - uxx = 0.